Long Term Voltage Stability
Maintaining steady voltage is one of the four rules that has to be complied to achieve modern power system reliability, according to the US DOE report Maintaining Reliability in the Modern Power System. The steady voltage is often related to the power system long-term voltage stability (or ''static'' voltage stability in some literatures) which is controlled by the reactive power injections at certain nodes in the power grid. Due to the nonlinearity of power system physics, the nodal voltage magnitude cannot be maintained in any arbitrary loading conditions. The transmission network naturally has a maximum power transfer limit. Any attempt to send or require more power than this physical limit will result in unstoppable voltage declines. This phenomenon is called the voltage collapse.
Challenges from Distributed Renewable Energy
To evaluate how far the current operation condition is away from voltage collapse, system operators numerically simulate the system's quasi steady state trajectory by continuously increasing the power demand and generation for a few expected typical future scenarios. In the future when renewable generation largely replaces fossil fuel generation in a distributed manner, it creates an ultra high dimensional operation space with numerous unobservable (or uncontrollable) local devices and much higher uncertainty in large dispersion. Thus, traditional methods to evaluate typical load and generation scenarios will become less effective in enumerating all the possibilities that the system may face.
Searching for the Shortest Path to Voltage Collapse
In order to secure the reliability of the future power grid, an alternative methodology needs to be considered: finding the worst scenario among all the possibilities. Some work has proposed an optimization framework that can seek for the minimum voltage stability margin among all the load and generation scenarios. The voltage stability margin was assigned by the Eucliean metric in the power injection subspace. This margin ignores the manifold curvature change for which the power system physics intrinsically defined, resulting in misleading voltage stability information. For example, we have revealed that the power flow model can admit multiple disconnected singular boundaries, only one of which contributes to the voltage collapse, others do not. However, the global minimum with respect to the Euclidean metric tends to be on the wrong singular boundaries (shown by the following left plot). Moreover, even when an Euclidean local minimum is on the correct singular boundary, it may not be the shortest path to voltage collapse on the manifold (shown by the following right plot).
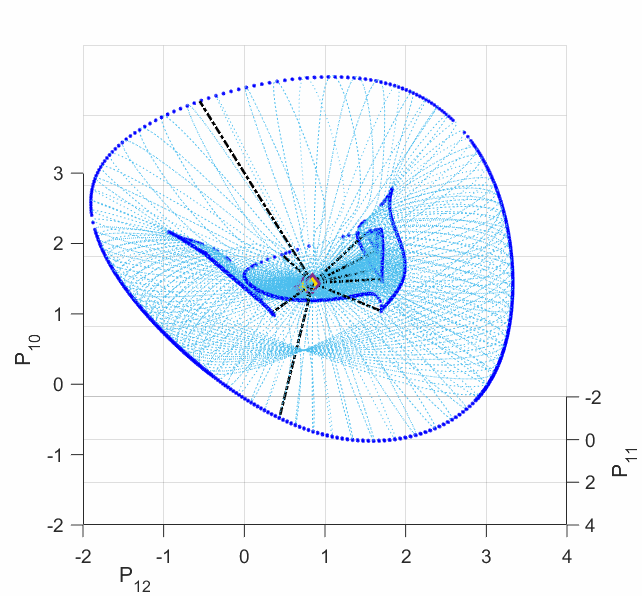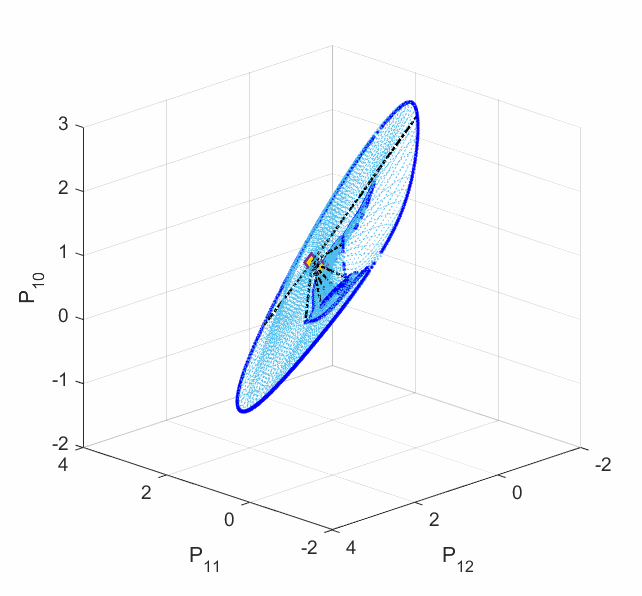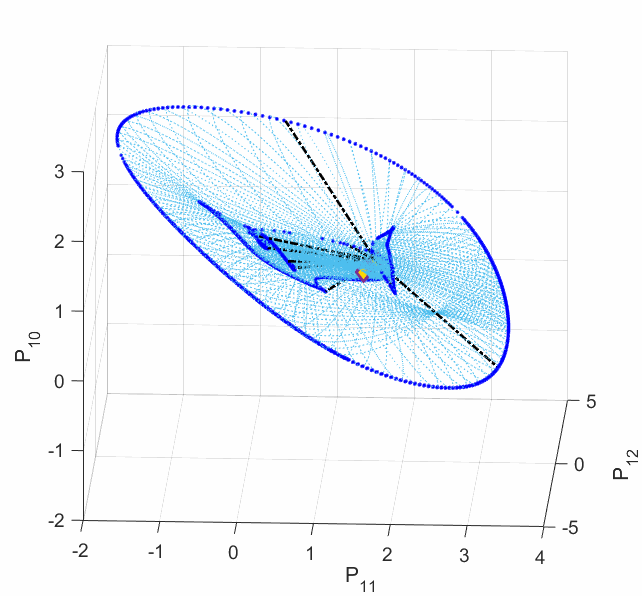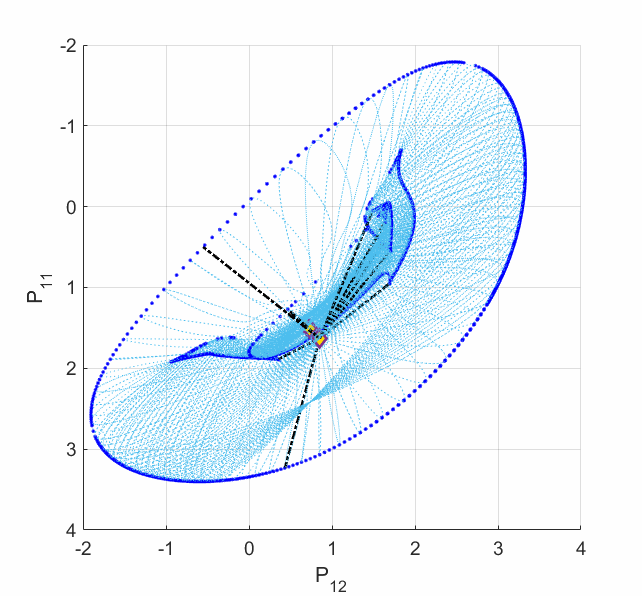
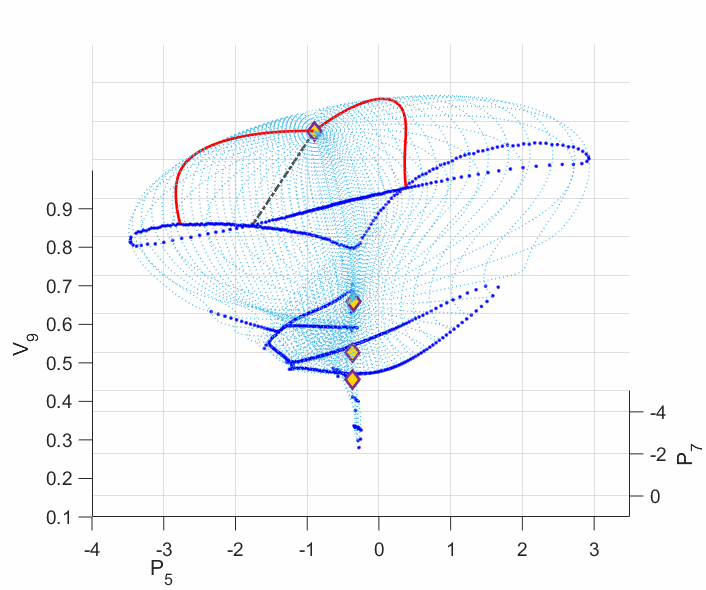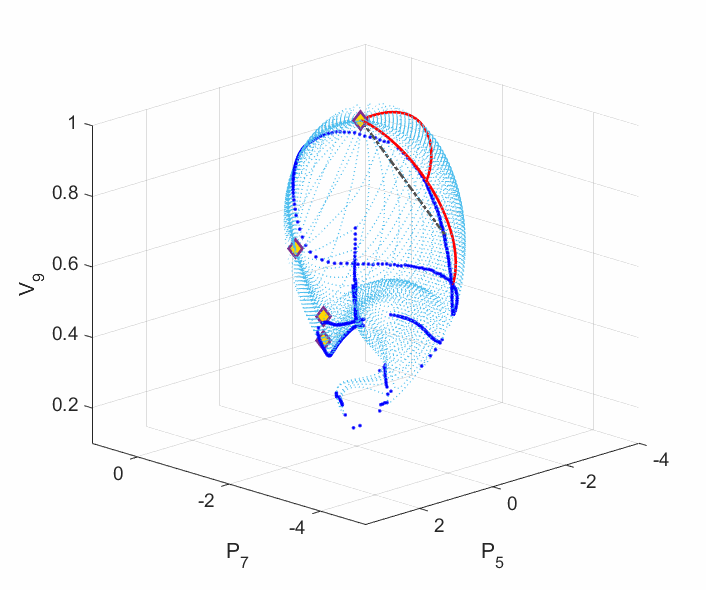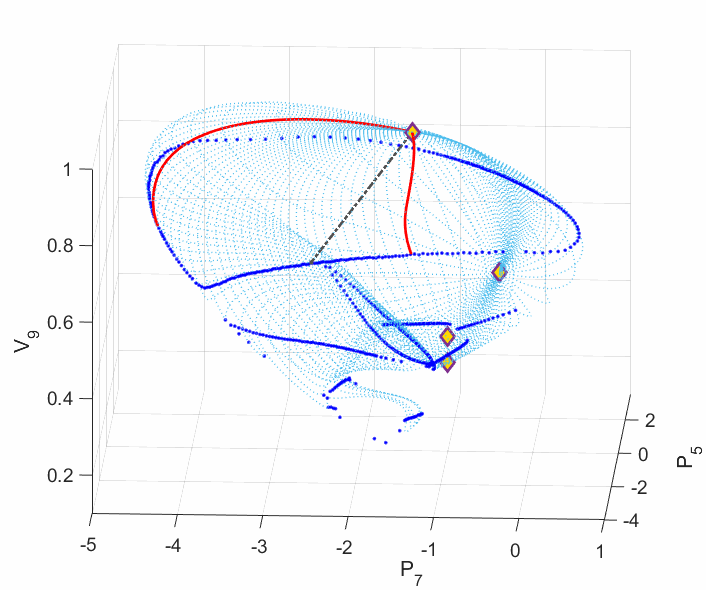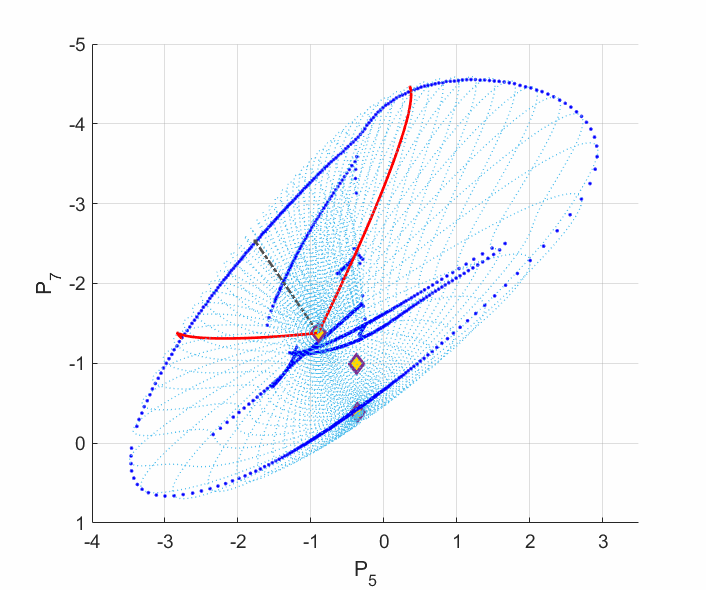
Left Plot: The deep blue curves are the singular boundaries, among which the outer one constributes to the voltage collapse. Five local minima are shown in dashed line segments. One can see from the plot that the Euclidean global minimum ends on the inner boundary, which does not contribute to the voltage collapse. This is a very common phenomenon exhibited by most (if not all) IEEE standard test cases.
Right Plot: The red curves are the two locally shortest paths to the voltage collapse boundary on the manifold. The dashed line segment is the closest Euclidean local minimum to these red paths ending on the same singular boundary. The Euclidean local minimum deviates from the shortest paths on the manifold a lot, which yields misleading voltage stability margin and a wrong power changing direction.
To better characterize the shortest path to voltage collapse on the manifold, we completely transfer the long-term voltage stability margin from the Euclidean metric to the Riemann metric. This ''subtle'' change has largely increased the complexity of the problem. To make an analogy, imagine we are in a valley surrounded by many mountains. We are supposed to find the shortest trail going out of these surrounding mountains. However, we even don't know where the peak ridges are unless we reach them. To solve this problem, we further converted it into an optimal control framework, and applied out-of-shelf optimal control solvers for the solution. We have shown that by using the Riemann metric the global minimum on the manifold can only be on the correct singular boundary. Technical results and detailed discussions can be found in Searching for the Shortest Path to Voltage Instability Boundary: from Euclidean Space to Algebraic Manifold. Our current work has scaled this method up to power grids with thousands of nodes by innovative approximation techniques with high accuracy and low execution time (several minutes).