Power System Oscillations

Sustained oscillations are observed very frequently in today's power grids. For example, the following plots present two real oscillation cases recorded by the NEISO. The raw data and other real cases can be found here. 

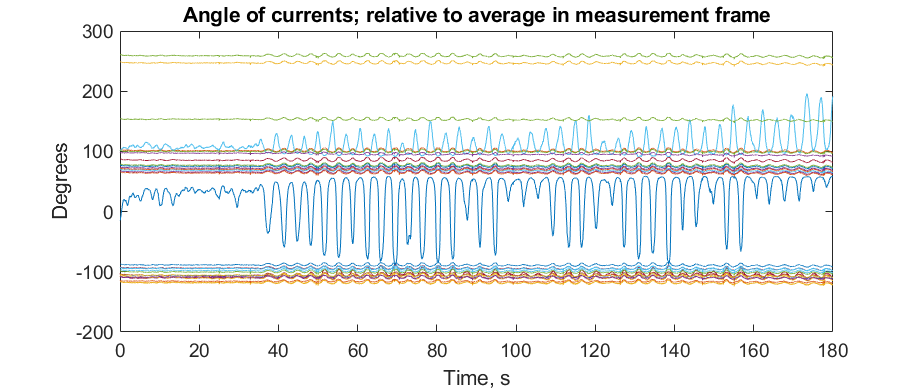
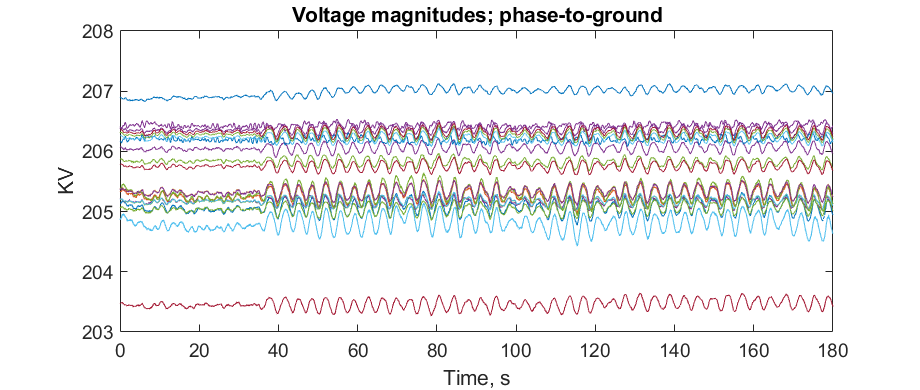
These oscillations, if not treated properly, can deteriorate power system service quality, and even lead to instability. 

Nonlinear Oscillations

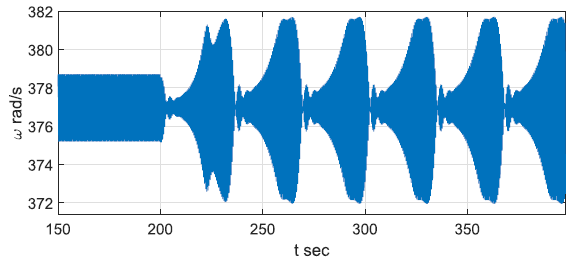
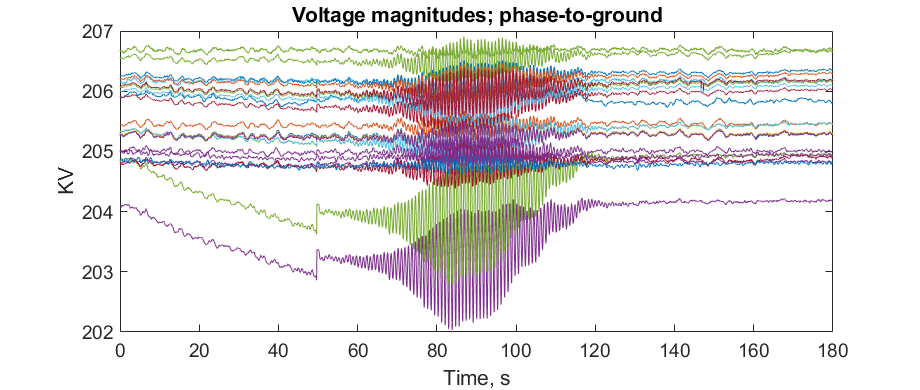
Although the nominal operating point of a power grid is in the linearly designed engineering region, oscillations can make the operating point largely deviate from this linear region, exhibiting strong nonlinear phenomena. For example, the following plots show the strong nonlinearity of a sustained oscillation from the above mentioned real case archive. 

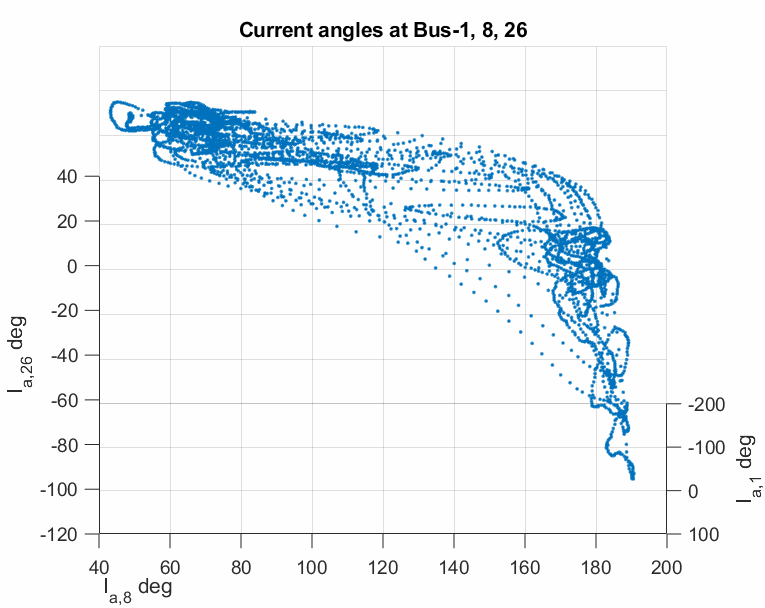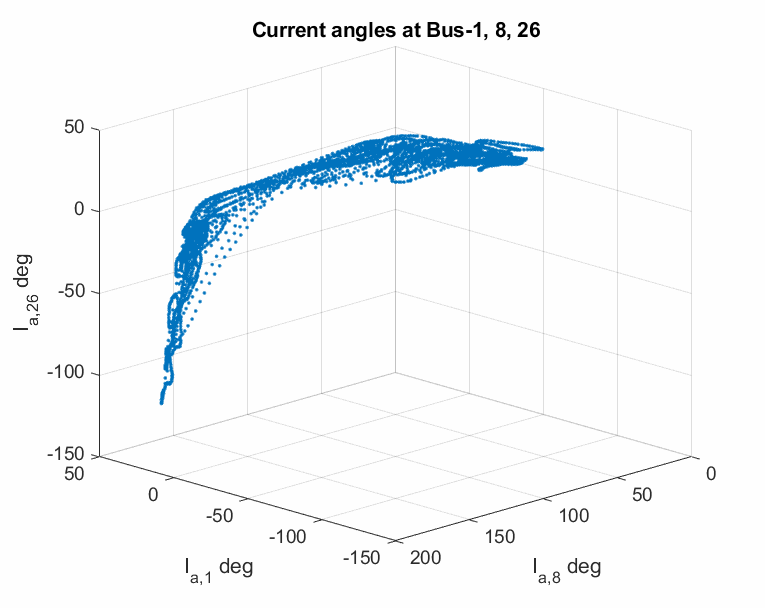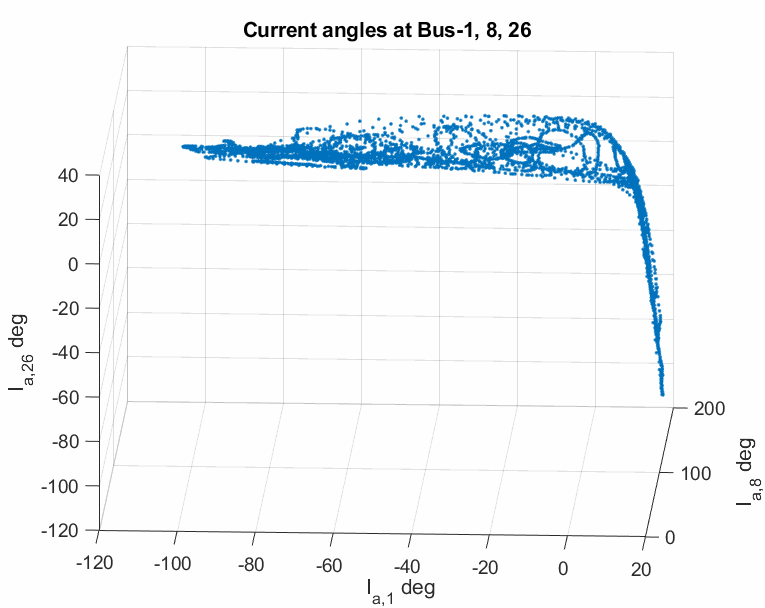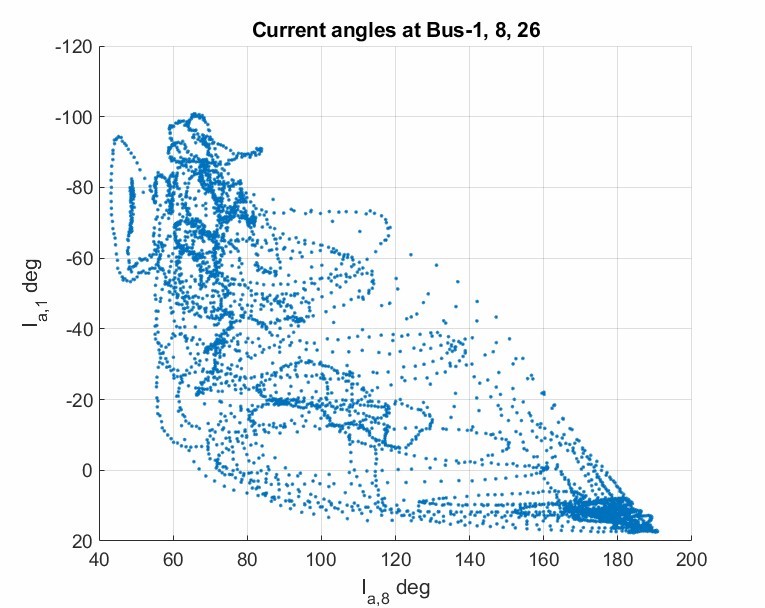
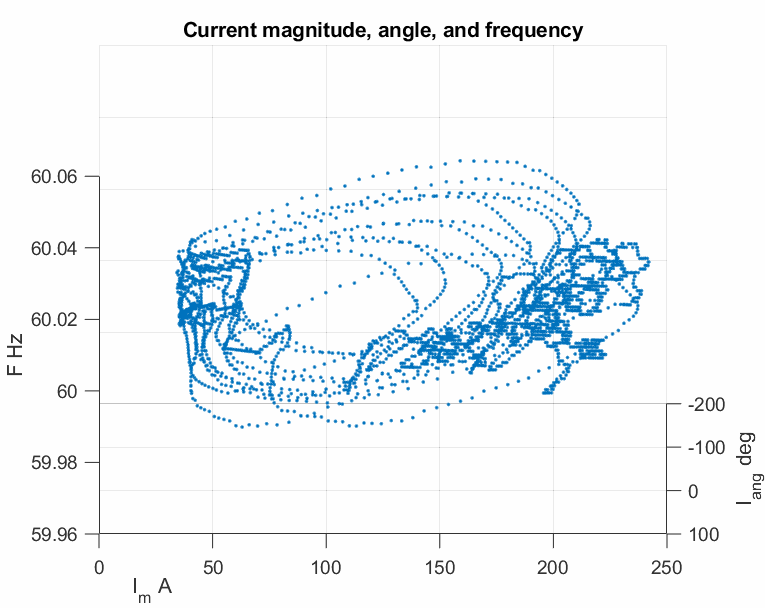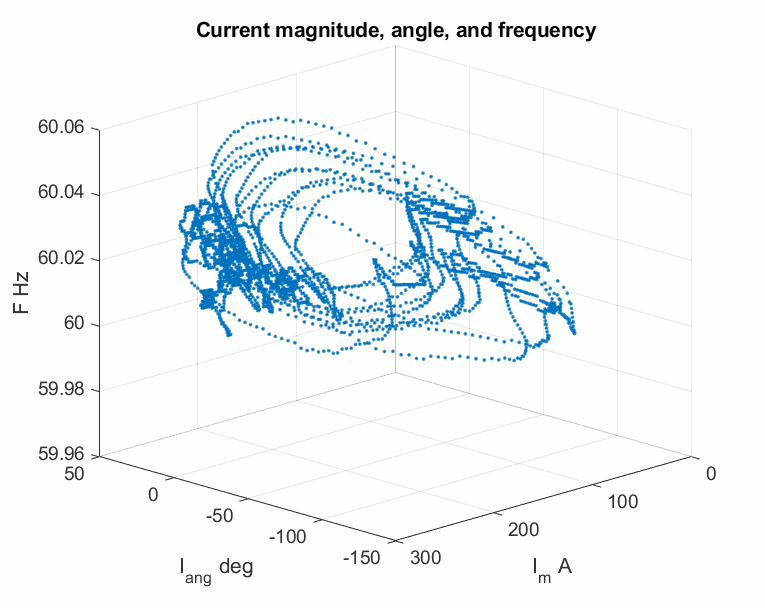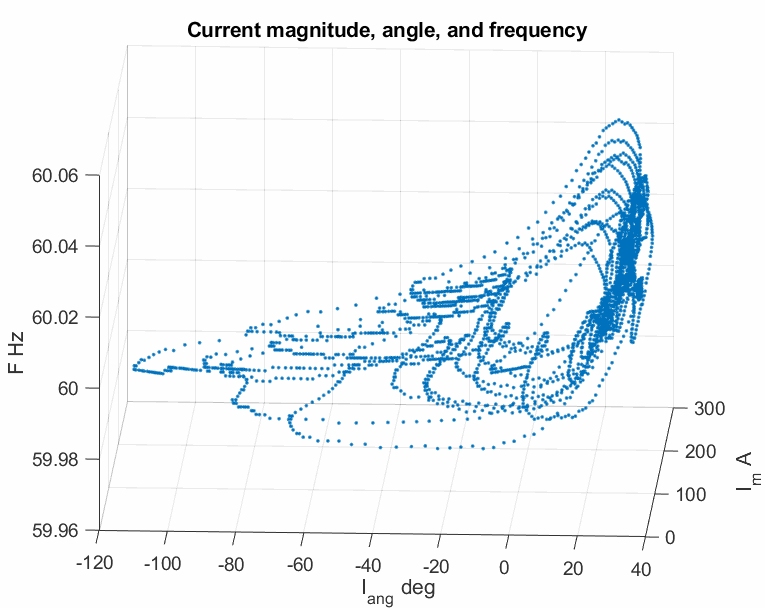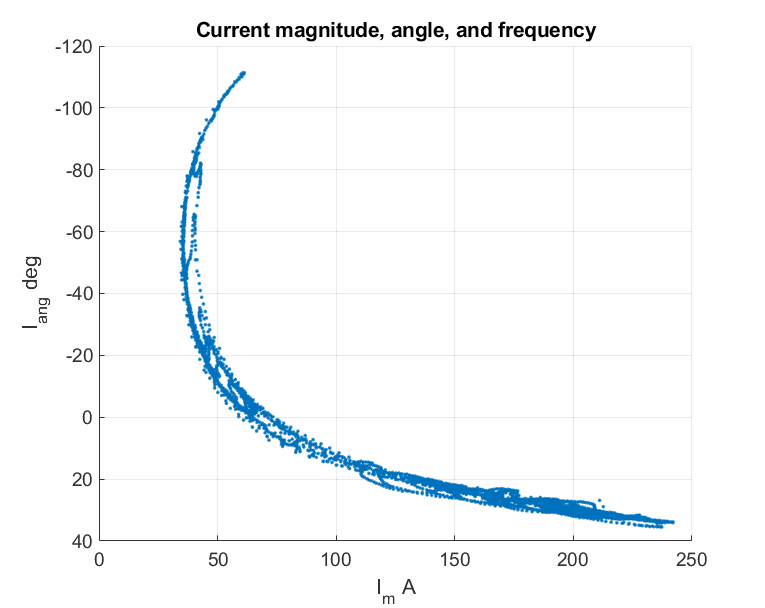
The modulated oscillation is one of those nonlinear oscillations that have been observed by the real PMU data in power grids. A representative plot is shown below.

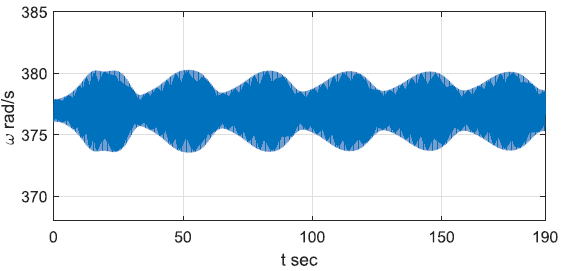
Besides the basic oscillatory frequency, the modulated oscillation superimposes another frequency which forms the modulated waveform of the envelope of the basic oscillation. This phenomenon has been observed more frequently in recent years with the inverter-based generation. It is evolved from a basic sustained oscillation, and has nonlinear interactions in principle.

Neimark-Sacker Bifurcation and Chenciner Bifurcation

In the work Modulated Oscillations of Synchronous Machine Nonlinear Dynamics With Saturation, we have shown that such nonlinear oscillations come from the Neimark-Sacker bifurcation (a.k.a. the torus bifurcation), which converts a limit cycle into a torus. It is strongly related to the flux saturation of the field winding in synchronous machines. More interestingly, a new bifurcation type called the Chenciner bifurcation has also been reported in the paper. It is a degenerate case of the Neimark-Sacker bifurcation which can create two stable attractors (shown by the following left plot) for the system in a certain parameter region (shown in the left region of the following right plot) rather than just at the bifurcation point. 

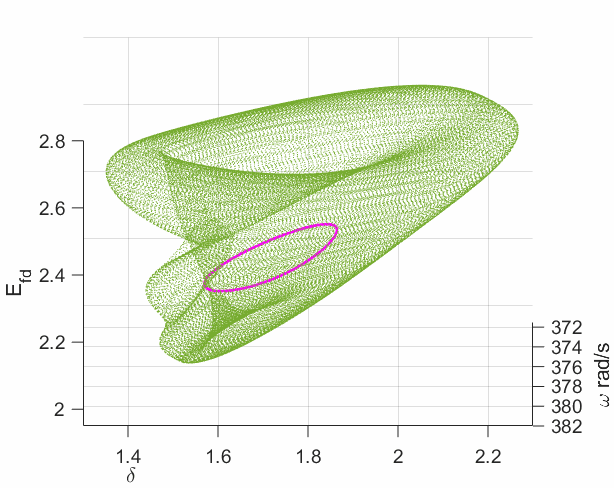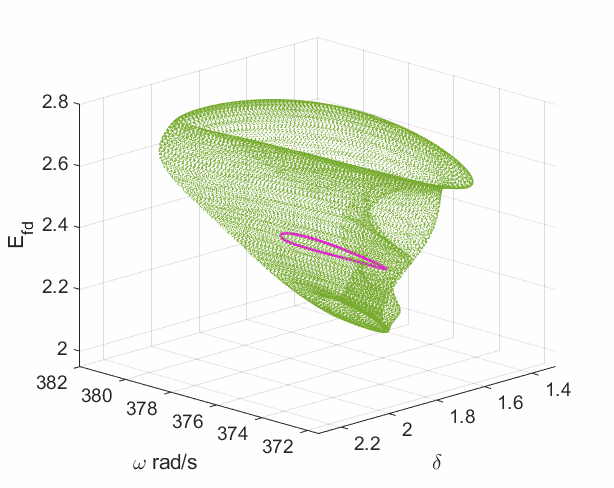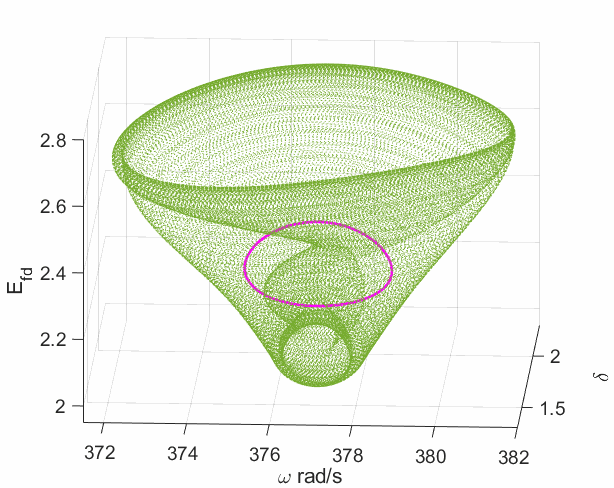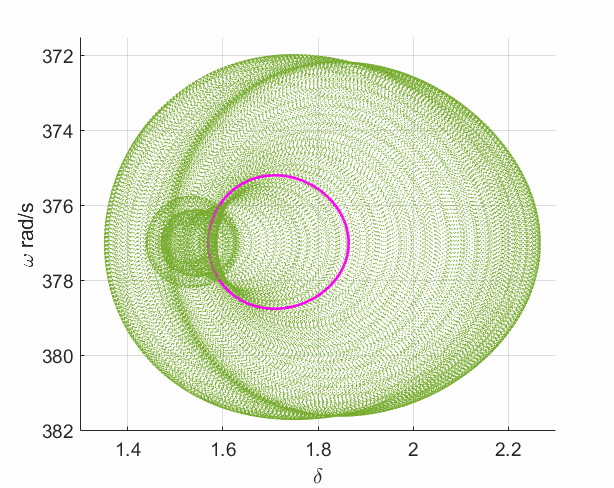
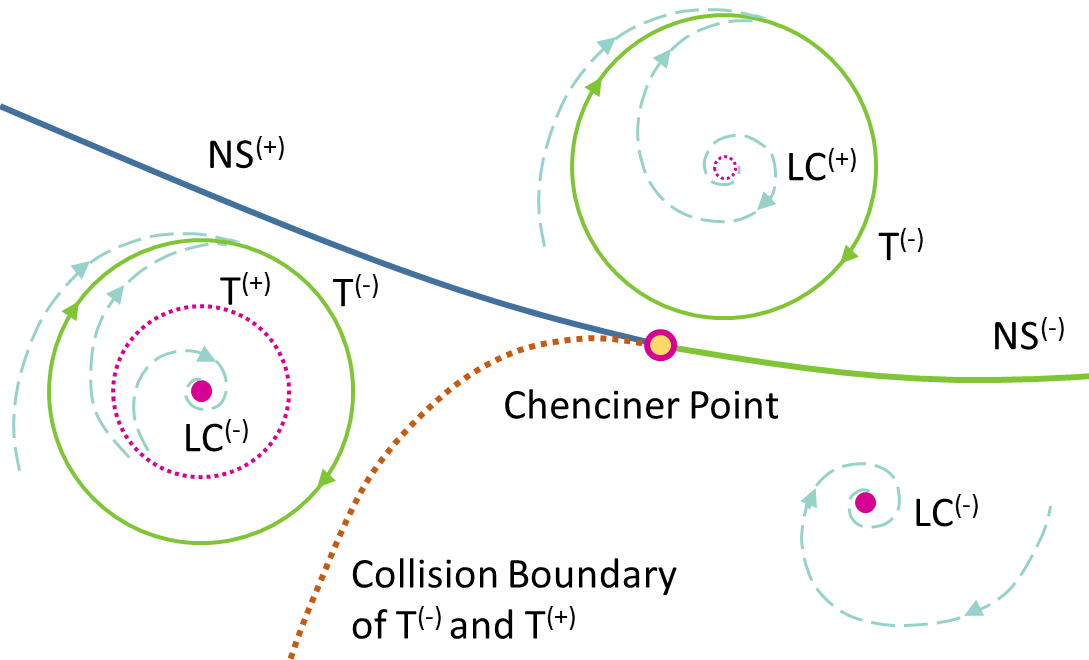
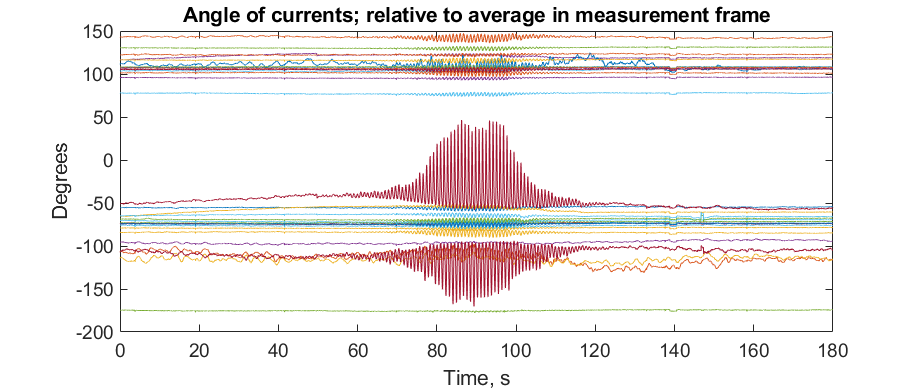
It indicates that a temporary disturbance (disappear very quickly) can change the power system oscillatory type from a limit cycle into a torus without changing any parameters (no touching any bifurcation condition). It may give an explanation of some cases when a sustained oscillation suddenly jumped into a modulation mode, as shown below.