Power System Cascading Failures
Power systems frequently experience random disturbances from the environment, such as falling tree branch induced short circuits, lightnings, etc, causing temporary local faults. To protect power system apparatus not being damaged from these faults, relay protections are widely used to disconnect the corresponding equipments during faults. This event is called a contingency. Modern power grid operations are scheduled to pass the N-1 contingency test, which requires the system to keep a post-fault normal operation whatever a single equipment is out of service. However, there are cases when an initial failure (may have multiple contingencies) induces subsequent failures. This sequence of failures is called the cascading failure (or failure cascade). It usually ends up with a regional blackout, for example, the 2003 North America Blackout.
In the near future when the renewables become a major energy resource in power generation, the power grid will encounter much severe intermittent disturbances with wide spatial-temporal dispersion. This situation can largely increase probabilities of N-k contingencies (k>1) which are not addressed by the traditional N-1 contingency analysis, resulting in high risks of cascading failures and blackouts.
Failure Cascade Simulators by Learning Methods
To reduce the risk of failure cascades for the future power grid, N-k contingencies should be evaluated. However, in a large-scale power system the complexity of evaluating N-k contingencies is combinatorial. Therefore, we need more efficient methods to (1) quickly simulate large quantities of N-k contingencies, (2) easily identify the most critical initial failures.
A Markovian-like model called the Influence Model was proposed in the literature the Influence Model. It can be interpreted as a probabilistic model predicting each component's status for the next time step based on current status of all compoents. It avoids solving the power flow problem at each time step, and thus, can be much more efficient than the power flow-based failure cascade simulators. To achieve a high prediction accuracy, the mutual influence parameters and the accumulative weights of the influence model need to be identified. In the paper Predicting Failure Cascades in Large Scale Power Systems via the Influence Model Framework, we proposed a hybrid learning method that combines the Monte-Carlo method, the quadratic programming, and the adaptive threshold value selection scheme to better enhance the prediction accuracy of the influence model. With limited training samples, the proposed method is capable of predicting the overall N-2 contingency induced failure cascade size with an error rate up to 7%, the final state of links with an error rate up to 10%, and the failure time within 1 time unit for large-scale power systems with thousands of nodes. The failure cascade simulation has been speed-up beyond 800X for some large-scale power system AC models. The learned influence values can also be used to easily identify the critical components whose failures can lead to large-scale failure cascades. A sample simulated failure cascade process is shown in the following plot.

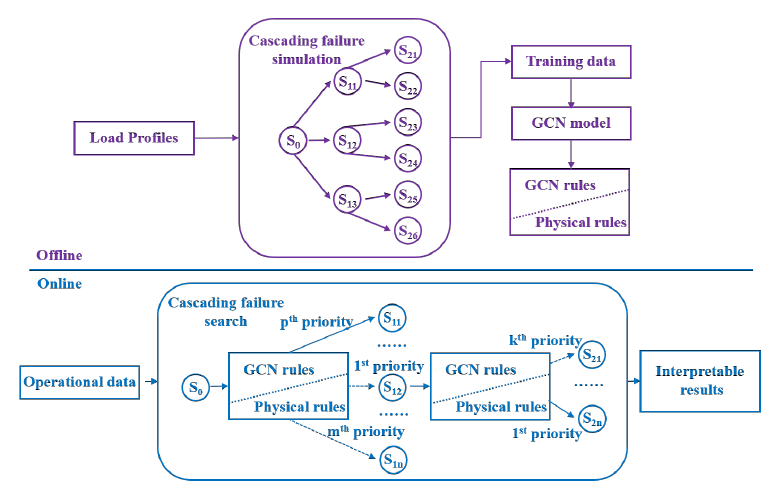
To better identify the critical initial failures from multiple factors, in the work Searching for Critical Power System Cascading Failures with Graph Convolutional Network we proposed a Graphic Convolutional Network (GCN) based learning method. An illustration of the proposed GCN framework is shown below. Four different factors, network topology, protection, line flow, and load, are simultaneously fed into the machine to acquire a comprehensive critical contingency identification. Considering the sparse connectivity of power grids, the GCN is favorable of reducing the parameter space of the learning method when compared to the DNN or CNN. This method has been testified on a real-world regional power grid with 1500 transmission lines.